Uncertainty Unveiled: A Probabilistic Approach to Volumetrics
In the world of oil and gas exploration, accurately estimating the potential volumes of hydrocarbons deposited in the earth's surface is paramount. This process is a known as volumetrics.
The process hinges on a series of key inputs that describe the reservoir's size and its fluid content. A deterministic approach has been used intially, plugging single "best guess" values into a straightforward equation. However, this method often presents an overly simplistic view, failing to acknowledge the inherent uncertainties that permeate the exploration phase.
The Ingredients
To estimate the Hydrocarbons Initially In Place (HIIP) – whether Gas Initially In Place (GIIP) or Oil Initially In Place (OIIP), often referred to as stock tank oil – a fundamental calculation is employed. This equation relies on several crucial parameters:
GRV (Gross Rock Volume): Measured in cubic feet (ft³) or cubic meters (m³), GRV represents the entire volume of rock that could contain hydrocarbons. It's typically the first output from seismic interpretation software, outlining the boundaries of the potential reservoir, either area-depth method or area-thickness method are used.
NTG (Net-to-Gross): Not all the rock within the GRV is actually filled with hydrocarbons. NTG, usually derived from well logs (often nearby, analogous wells), acts as a filter. It's the fraction or percentage of the GRV that represents the productive reservoir rock.
Porosity (Φ): Think of the tiny spaces within the reservoir rock that can hold fluids. Porosity, also typically estimated from well logs of nearby wells, quantifies the percentage of this rock volume that is pore space.
Water Saturation (Sw): Within those pore spaces, not all the fluid is oil or gas. Water saturation, again usually derived from well logs, tells us the fraction of the pore space occupied by water. Therefore, the hydrocarbon saturation is (1 - Sw).
FVF (Formation Volume Factor): This factor accounts for the changes in volume that hydrocarbons undergo as they are brought from the high-pressure, high-temperature reservoir conditions to the surface.
Bo (Oil Formation Volume Factor): Recognizes that once dissolved gas is liberated from oil during production, the oil volume shrinks at the surface compared to its volume in the reservoir.
Bg (Gas Formation Volume Factor): Also known as the inverse of the gas expansion factor, Bg accounts for the significant expansion of gas as it rises to the surface.
Ignoring Uncertainties
Once these input data are gathered, a deterministic estimate of HIIP can be calculated through simple multiplication. However, the major drawback of this approach is that it yields only a single, fixed value. In the early exploration phase, where data is often sparse and reliant on offset wells (wells drilled nearby), significant uncertainty surrounds each of these input parameters. Relying on a single "best guess" ignores this inherent variability and provides a potentially misleading sense of precision.
The Power of Probabilistic Volumetrics
To address this limitation, a probabilistic approach offers a more robust and realistic assessment. Instead of single values, each of the variables mentioned above (GRV, NTG, Porosity, Water Saturation, FVF) is treated as a range of possible values defined by a probability density function (PDF).
The shape of these PDFs – often normal, lognormal, gamma, or beta distributions – reflects the level of uncertainty associated with each variable and its likely distribution. For instance, a variable with high confidence might have a narrow, bell-shaped (normal) distribution centered around the best estimate, while a more uncertain variable might have a wider, flatter distribution.
For simplicity I have been using only normal distributions.
Probability Distribution of HIIP
After defining these probabilistic ranges for each input, the volumetric equation is run numerous times – often tens or hundreds of thousands of iterations – using random values sampled from the defined PDFs for each variable in each iteration. This is akin to exploring all the possible combinations of input values within their estimated ranges.
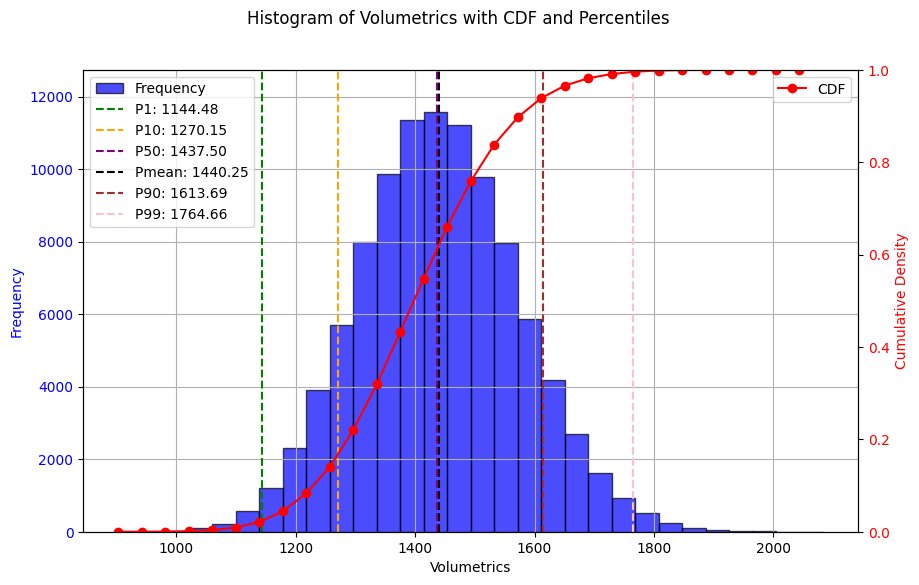
It's crucial to run these simulations a sufficient number of times to ensure the results converge, providing a stable and representative distribution of potential HIIP values. The final output is not a single number, but a probability distribution curve, like the one you mentioned after 100,000 runs.
This distribution provides a much richer understanding of the potential resource:
P90: Represents a high probability (90%) that the actual HIIP will be greater than or equal to this value (a conservative estimate).
P50: Represents a 50% probability that the actual HIIP will be greater than or equal to this value (the median or most likely estimate).
P10: Represents a low probability (10%) that the actual HIIP will be greater than or equal to this value (an optimistic estimate).
From Exploration to Development: Refining the Volume Picture
This probabilistic approach is particularly valuable in the early exploration phase, both before and after drilling an initial well. As more data becomes available – such as detailed well logs and reservoir tests – a more refined static reservoir model can be built.
In my experience at a previous company, we adhered to a guideline that the P50 probabilistic volumetric estimate should not deviate by more than +/- 20% from the base case deterministic static model built after initial drilling. This served as a quality check on the consistency between the early probabilistic assessments and the more detailed static models.
It's also common practice to construct additional deterministic scenarios based on the refined static model: a low-case and a high-case. However, these deterministic scenarios often involve simply degrading or upgrading key reservoir properties across the entire model, which might not fully capture the complex spatial variability and uncertainties within the reservoir.
Conclusion: Embracing Uncertainty for Informed Decisions
By moving beyond single-point estimates and embracing the power of probabilistic volumetrics, we gain a more realistic understanding of the potential hydrocarbon resources and the associated risks. This allows for more informed decision-making in the high-stakes game of oil and gas exploration, ultimately leading to better resource management and more successful ventures.
The next step would be to multiply this equation with the recovery factor (RF), which should be also defined through distribution curve, based on information from analogue fields and additional information from the reservoir engineer.